СВОБОДНОЕ ПАДЕНИЕ ТЕЛА С УЧЕТОМ СОПРОТИВЛЕНИЯ СРЕДЫ
При реальных физических движениях тел в газовой или жидкостной среде трение накладывает огромный отпечаток на характер движения. Каждый понимает, что предмет, сброшенный с большой высоты (например, парашютист, прыгнувший с самолета), вовсе не движется равноускоренно, так как по мере набора скорости возрастает сила сопротивления среды. Даже эту. относительно несложную, задачу нельзя решить средствами «школьной» физики; таких задач, представляющих практический интерес, очень много. Прежде чем приступать к обсуждению соответствующих моделей, вспомним, что известно о силе сопротивления.
Закономерности, обсуждаемые ниже, носят эмпирический характер и отнюдь не имеют столь строгой и четкой формулировки, как второй закон Ньютона. О силе сопротивления среды движущемуся телу известно, что она, вообще говоря, растет с ростом скорости (хотя это утверждение не является абсолютным). При относительно малых скоростях величина силы сопротивления пропорциональна скорости и имеет место соотношение Fcoпp = k1v, где k1 определяется свойствами среды и формой тела. Например, для шарика k1 = 6??r - это формула Стокса, где ?
-динамическая вязкость среды, r -
радиус шарика. Так, для воздуха при t
= 20°С и давлении 1 атм.? = 0,0182 Н•с•м-2, для воды 1,002 Н•с•м-2, для глицерина 1480 Н•с•м-2.
Оценим, при какой скорости для падающего вертикально шара сила сопротивления сравняется с силой тяжести (и движение станет равномерным).
Имеем
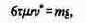
или

Пусть r
= 0,1 м, ? = 0,8•103
кг/м3 (дерево). При падении в воздухе v* ? 960 м/с, в воде v*? 17 м/с, в глицерине v* ? 0,012 м/с.
На самом деле первые два результата совершенно не соответствуют действительности. Дело в том, что уже при гораздо меньших скоростях сила сопротивления становится пропорциональной квадрату скорости: Fcoпp
= k2v2. Разумеется, линейная по скорости часть силы сопротивления формально также сохранится, но если k2v2>> k1v, то вкладом k1v можно пренебречь (это конкретный пример ранжирования факторов).
О величине k2 известно следующее: она пропорциональна площади сечения тела S,
поперечного по отношению к потоку, и плотности среды ?среды и зависит от формы тела. Обычно представляют k2
= 0,5сS?срeды, где с - коэффициент лобового сопротивления - безразмерен. Некоторые значения с (для не очень больших скоростей) приведены на рис. 7.6.
При достижении достаточно большой скорости, когда образующиеся за обтекаемым телом вихри газа или жидкости начинают интенсивно отрываться от тела, значение с в несколько раз уменьшается; для шара оно становится приблизительно равным 0,1. Подробности можно найти в специальной литературе.
Вернемся к указанной выше оценке, исходя из квадратичной зависимости силы сопротивления от скорости.
Имеем
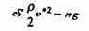
или
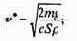
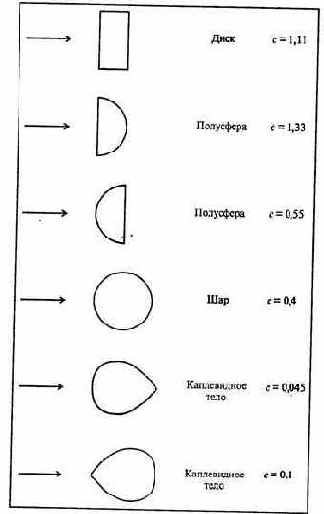
Рис. 7.6. Значения коэффициента лобового сопротивления для некоторых тел, поперечное сечение которых имеет указанную на рисунке форму (см. книгу П.А.Стрелкова)
Для шарика
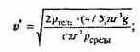
Примем r = 0,1 м, ? = 0,8•103 кг/м3 (дерево). Тогда для движения в воздухе (?возд= 1,29 кг/м3) получаем v*
? 18 м/с, в воде (?воды ? 1•103 кг/м3) v* ? 0,65 м/с, в глицерине (?глицерина = 1,26•103
кг/м3) v* ? 0,58 м/с.
Сравнивая с приведенными выше оценками линейной части силы сопротивления, видим, что для движения в воздухе и в воде ее квадратичная часть сделает движение равномерным задолго до того, как это могла бы сделать линейная часть, а для очень вязкого глицерина справедливо обратное утверждение. Рассмотрим свободное падение с учетом сопротивления среды. Математическая модель движения - уравнение второго закона Ньютона с учетом двух сил, действующих на тело; силы тяжести и силы сопротивления среды:
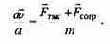
Движение является одномерным; проецируя векторное уравнение на ось, направленную вертикально вниз, получаем
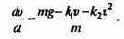
Вопрос, который мы будем обсуждать на первом этапе, таков: каков характер изменения скорости со временем, если все параметры, входящие в уравнение (7.7), заданы? При такой постановке модель носит сугубо дескриптивный характер.
Из соображений здравого смысла ясно, что при наличии сопротивления, растущего со скоростью, в какой-то момент сила сопротивления сравняется с силой тяжести, после чего скорость больше возрастать не будет. Начиная с этого момента, dv/dt = 0, и соответствующую установившуюся скорость

= 0 , решая не дифференциальное, а квадратное уравнение. Имеем
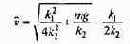
(второй - отрицательный - корень, естественно, отбрасываем). Итак, характер движения качественно таков: скорость при падении возрастает от v0
до

как и по какому закону - это можно узнать, лишь решив дифференциальное уравнение (7.7).
Однако, даже в столь простой задаче мы пришли к дифференциальному уравнению, которое не относится ни к одному из стандартных типов, выделяемых в учебниках по дифференциальным уравнениям, допускающих очевидным образом аналитическое решение. II хотя это не доказывает невозможность его аналитического решения путем хитроумных подстановок, но они не очевидны (один из лучших помощников в их поиске - справочник Камке). Допустим, однако, что нам удастся найти такое решение, выраженное через суперпозицию нескольких алгебраических и трансцендентных функций - а как найти закон изменения во времени перемещения? - Формальный ответ прост:
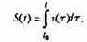
но шансы на реализацию этой квадратуры уже совсем невелики. Дело в том, что класс привычных нам элементарных функций очень узок, и совершенно стандартна ситуация, когда интеграл от суперпозиции элементарных функций не может быть выражен через элементарные функции в принципе. Математики давно расширили множество функций, с которыми можно работать почти так же просто, как с элементарными (т.е. находить значения, различные асимптотики, строить графики, дифференцировать, интегрировать). Тем, кто знаком с функциями Бесселя, Лежандра, интегральными функциями и еще двумя десятками других, так называемых, специальных функций, легче находить аналитические решения задач моделирования, опирающихся на аппарат дифференциальных уравнений.
Однако даже получение результата в виде формулы не снимает проблемы представления его в виде, максимально доступном для понимания, чувственного восприятия, ибо мало кто может, имея формулу, в которой сопряжены логарифмы, степени, корни, синусы и тем более специальные функции, детально представить себе описываемый ею процесс -а именно это есть цель моделирования.
В достижении этой цели компьютер - незаменимый помощник. Независимо от того, какой будет процедура получения решения - аналитической или численной, -задумаемся об удобных способах представления результатов. Разумеется, колонки чисел, которых проще всего добиться от компьютера (что при табулировании формулы, найденной аналитически, что в результате численного решения дифференциального уравнения), необходимы; следует лишь решить, в какой форме и размерах они удобны для восприятия. Слишком много чисел в колонке быть не должно, их трудно будет воспринимать, поэтому шаг, с которым заполняется таблица, вообще говоря, гораздо больше шага, с которым решается дифференциальное уравнение в случае численного интегрирования, т.е. далеко не все значения v и S,
найденные компьютером, следует записывать в результирующую таблицу (табл. 7.2).
Таблица 7.2
Зависимость перемещения и скорости падения «безпарашютиста» от времени (от 0 до 15 с)
|
t(c) |
s(m) |
v (м/с) |
t(с) |
S(м) |
v (м/с) |
|
0 |
0 |
0 |
8 |
200,1 |
35,6 |
|
1 |
4,8 |
9,6 |
9 |
235,9 |
36,0 |
|
2 |
18,7 |
17,9 |
10 |
272,1 |
36,3 |
|
3 |
40,1 |
24,4 |
11 |
308,5 |
36,4 |
|
4 |
66,9 |
28,9 |
12 |
345,0 |
36,5 |
|
5 |
97,4 |
31,9 |
13 |
381,5 |
36,6 |
|
6 |
130,3 |
33,8 |
14 |
418.1 |
36,6 |
|
7 |
164,7 |
35,0 |
15 |
454,7 |
36,6 |
по ним хорошо видно, как меняются со временем скорость и перемещение, т.е. приходит качественное понимание процесса.
Еще один элемент наглядности может внести изображение падающего тела через равные промежутки времени.
Ясно, что при стабилизации скорости расстояния между изображениями станут равными. Можно прибегнуть и к цветовой раскраске - приему научной графики, описанному выше.
Наконец, можно запрограммировать звуковые сигналы, которые подаются через каждый фиксированный отрезок пути, пройденный телом - скажем, через каждый метр или каждые 100 метров - смотря по конкретным обстоятельствам. Надо выбрать интервал так, чтобы вначале сигналы были редкими, а потом, с ростом скорости, сигнал слышался все чаще, пока промежутки не сравняются. Таким образом, восприятию помогают элементы мультимедиа. Поле для фантазии здесь велико.
Приведем конкретный пример решения задачи о свободно падающем теле. Герой знаменитого фильма «Небесный тихоход» майор Булочкин, упав с высоты 6000 м в реку без парашюта, не только остался жив, но даже смог снова летать. Попробуем понять, возможно ли такое на самом деле или же подобное случается только в кино. Учитывая сказанное выше о математическом характере задачи, выберем путь численного моделирования. Итак, математическая модель выражается системой дифференциальных уравнений
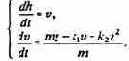
Разумеется, это не только абстрактное выражение обсуждаемой физической ситуации, но и сильно идеализированное, т.е. ранжирование факторов перед построением математической модели произведено. Обсудим, нельзя ли произвести дополнительное ранжирование уже в рамках самой математической модели с учетом конкретно решаемой задачи, а именно - будет ли влиять на полет парашютиста линейная часть силы сопротивления и стоит ли ее учитывать при моделировании.
Так как постановка задачи должна быть конкретной, мы примем соглашение, каким образом падает человек. Он - опытный летчик и наверняка совершал раньше прыжки с парашютом, поэтому, стремясь уменьшить скорость, он падает не «солдатиком», а лицом вниз, «лежа», раскинув руки в стороны. Рост человека возьмем средний - 1,7 м, а полуобхват грудной клетки выберем в качестве характерного расстояния - это приблизительно 0,4 м.
Для оценки порядка величины линейной составляющей силы сопротивления воспользуемся формулой Стокса. Для оценки квадратичной составляющей силы сопротивления мы должны определиться со значениями коэффициента лобового сопротивления и площадью тела. Выберем в качестве коэффициента число с = 1,2 как среднее между коэффициентами для диска и для полусферы (выбор для качественной оценки правдоподобен). Оценим площадь: S =
1,7•0,4=0,7 (м2).
Выясним, при какой скорости сравняются линейная и квадратичная составляющие силы сопротивления. Обозначим эту скорость v**. Тогда
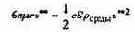
или

Ясно, что практически с самого начала скорость падения майора Булочкина гораздо больше, и поэтому линейной составляющей силы сопротивления можно пренебречь, оставив лишь квадратичную составляющую.
После оценки всех параметров можно приступить к численному решению задачи. При этом следует воспользоваться любым из известных численных методов интегрирования систем обыкновенных дифференциальных уравнений: методом Эйлера, одним из методов группы Рунге - Кутта, одним из многочисленных неявных методов. Разумеется, у них разная устойчивость, эффективность и т.д. - эти сугубо математические проблемы здесь не обсуждаются. Программа, реализующая метод Рунге - Кутта четвертого порядка, может быть взята из примера, приведенного в следующем параграфе или из какого-нибудь стандартного пакета математических программ.
Отметим, что существует немало программ, моделирующих простые физические процессы типа рассматриваемого. У них реализован, в той или иной мере профессионально, диалоговый интерфейс, позволяющий вводить параметры, получать на экране таблицы, графики, движущиеся изображения. Однако в них, как правило, остаются скрытыми физические законы, определяющие процесс, ограничения модели, возможности ее усовершенствования. Такие программы полезны скорее как сугубо иллюстративные.
Вычисления производились до тех пор, пока «безпарашютист» не опустился на воду. Примерно через 15 с после начала полета скорость стала постоянной и оставалась такой до приземления (рис. 7.7).
Отметим, что в рассматриваемой ситуации сопротивление воздуха радикально меняет характер движения; при отказе от его учета график скорости, изображенный на рисунке, заменился бы касательной к нему в начале координат.
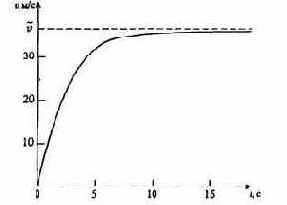
Рис. 7.7. График зависимости скорости падения «безпарашютиста» от времени
В некоторых случаях для ускорения процесса работы над какой-либо задачей целесообразно вместо составления программы воспользоваться готовой прикладной программой (например, табличным процессором). Покажем это на примере рассматриваемой задачи. В табл. 7.3 представлен небольшой фрагмент из табличного процессора Excel. Решение находится с помощью, так называемого, исправленного метода Эйлера - одного из возможных вариантов метода Рунге - Кутта второго порядка.
Кроме того, в ячейках D2, D4, D6 в таблице будем хранить соответственно значения шага вычислений, массы «безпарашютиста», величины mg. Это связано с тем, что все константы также удобно хранить в отдельных ячейках, чтобы в случае их изменения не пришлось переписывать расчетные формулы. Достаточно записать
Таблица 7.3
Фрагмент таблицы, где представлено решение задачи о «безпарашютнсте»
|
А |
В |
|
|
1 |
t |
v |
|
2 |
||
|
3 |
0 |
0 |
|
4 |
=СУММ(АЗ; D2) |
=B3+D2/2* ( (D6-D8*B3^2) /D4+(D6-D8*(B3+D2*(D6-D8*B3^2)/D4)^2)/D4) |
|
5 |
=СУММ(А4; D2) |
=B4+D2/2* ( (D6-D8*B4^2) /D4+(D6-D8* (B4+D2* (D6- D8*B4^2)/D4)^2)/D4) |
|
6 |
=СУММ(А5; D2) |
=B5+D2/2*( (D6-D8*B5^2)/D4+(D6-D8*(B5+D2*(D6-D8*B5^2)/D4)^2)/D4) |
|
7 |
=СУМM(А6; D2) |
=B6+D2/2* ( (D6-D8*B6^2) /D4+ (D6-D8* (B6+D2* (D6-D8*B6^2)/D4)^2)/D4) |
|
8 |
=СУММ(А7; D2) |
=B7+D2/2*((D6-D8*B7^2)/D4+(D6-D8*(B7+D2*(D6-D8*B7^2)/D4)^2)/D4) |
Таблица 7.4
Результаты вычислений, выполненных в табличном процессоре
|
А |
В |
С |
D |
|
|
1 |
t |
v |
H |
|
|
2 |
0,001 |
|||
|
3 |
0 |
0 |
т |
|
|
4 |
0,001 |
0,00981 |
80 |
|
|
5 |
0,002 |
0,01962 |
m*g |
|
|
6 |
0,003 |
0,02943 |
784,8 |
|
|
7 |
0,004 |
0,03924 |
k2 |
|
|
8 |
0,005 |
0,04905 |
0,55083 |
|
|
9 |
0,006 |
0,05886 |
Следует заметить, что для хранения результатов расчетов в данном случае требуется очень много ячеек таблицы, и хотя современные табличные процессоры позволяют хранить большой объем информации, в случае нехватки памяти рекомендуется увеличить шаг, с которым проводятся вычисления (при этом пожертвуем точностью вычислений). Табличный процессор позволяет представлять результаты расчетов и в графической форме. Можно при работе над задачей получить результаты двумя способами: с помощью табличного процессора и составлением собственной программы - для того. чтобы затем сравнить эти результаты и временные затраты каждого из способов. Но, несмотря на успешное применение табличного процессора при решении простейшей учебной задачи, следует признать, что для решения более громоздких в вычислительном плане задач предпочтительнее программировать самим. А теперь ответим на вопрос, поставленный в задаче. Известен такой факт: один из американских каскадеров совершил прыжок в воду с высоты 75 м (Бруклинский мост), и скорость приземления была 33 м/с. Сравнение
этой величины с получившейся у нас конечной скоростью 37,76 м/с позволяет считать описанный в кинофильме эпизод вполне возможным. Обсуждаемой модели можно придать черты оптимизационной, поставив задачу так: парашютист прыгает с некоторой высоты и летит, не открывая парашюта; на какой высоте (или через какое время) ему следует открыть парашют, чтобы иметь к моменту приземления безопасную скорость? Или по-другому: как связана высота прыжка с площадью поперечного сечения парашюта (входящей в k2), чтобы скорость приземления была безопасной? Выполнение таких исследований многократно более трудоемко, нежели просто изучение одного прыжка при заказанных условиях.