СТРУКТУРИРОВАННЫЕ ТИПЫ ДАННЫХ
Описанные выше типы данных называют простыми. Основной признак, по которому можно определить величину простого типа, таков: одно имя - одно значение.
Значительно большие возможности заключают в себе структурированные данные, определяемые разработчиком программы (в пределах возможностей используемого им языка программирования), К структурированию данных разработчика программы толкает как логика прикладной задачи, так и чисто утилитарное соображение: при наличии в задаче большого количества входных и выходных данных отдельное именование каждого из них может оказаться практически невозможным.
Разумеется, действия разработчика алгоритма и программы ограничены возможностями того языка программирования, на который он ориентируется. В разных языках возможности структуризации переменных на уровне сложных структур не совпадают, но многие структуры давно стали традиционными и реализованы в большинстве практически используемых языков программирования.
Структурированные типы данных классифицируют по следующим основным признакам: однородная - неоднородная, упорядоченная - неупорядоченная, прямой доступ - последовательный доступ, статическая - динамическая. Эти признаки противостоят друг другу лишь внутри пары, а вне этого могут сочетаться.
Если все элементы, образующие структуру, однотипны (например - целые числа или символы), то структура является однородной; если же в ней «перепутаны» элементы разной природы (например, числа чередуются с символами), то неоднородной.
Структуру называют
упорядоченной, если, между ее элементами определен порядок следования. Примером упорядоченной математической структуры служит числовая последовательность, в которой у каждого элемента (кроме первого) есть предыдущий и последующий. Наличие индекса в записи элементов структуры уже указывает на ее упорядоченность (хотя индекс для этого не является обязательным признаком).
По способу доступа упорядоченные структуры бывают прямого и последовательного доступа. При прямом доступе каждый элемент структуры доступен пользователю в любой момент независимо от других элементов.
Глядя на линейную таблицу чисел мы можем списать или заменить сразу, допустим, десятый элемент. Однако, если эта таблица не на бумаге, а, скажем, каким-то образом записана на магнитофонную ленту, то сразу десятое число нам недоступно - надо сначала извлечь девять предшествующих. В последнем случае мы имеем дело с последовательным доступом.
Если у структуры размер (длина, количество элементов) не может быть изменен «на ходу», а фиксирован заранее, то такую структуру называют статической. Программные средства информатики иногда позволяют не фиксировать размер структуры, а устанавливать его по ходу решения задачи и менять при необходимости, что бывает очень удобно. Такую структуру называют динамической. Например, при описании закономерностей движения очереди в магазине мы не знаем заранее, сколько человек в ней будет в тот или иной момент, и соответствующую структуру данных (например, список фамилий участников очереди) лучше представлять динамической.
Массивы
Самым традиционным и широко известным из структурированных типов данных является массив
(иначе называемый регулярным типом) - однородная упорядоченная статическая структура прямого доступа.
Массивом называют однородный набор величин одного и того же типа, называемых компонентами массива, объединенных одним общим именем (идентификатором) и идентифицируемых (адресуемых) вычисляемым индексом.
Это определение подчеркивает, что все однотипные компоненты массива имеют одно и то же имя, но различаются по индексам, которые могут иметь характер целых чисел из некоторого диапазона, литер, перечисленных констант. Индексы позволяют адресовать компоненты массива, т.е. получить доступ в произвольный момент времени к любой из них как к одиночной переменной (рис. 1.32). Обычный прием работы с массивом - выборочное изменение отдельных его компоневт.
Вычисляемые индексы позволяют использовать единое обозначение элементов массива для описания массовых однотипных операций в циклических конструкциях программ.
Важной особенностью массива является его статичность. Массив должен быть описан в программе (т.е. определены тип и число компонент) и его характеристики не могут быть изменены в ходе выполнения программы.
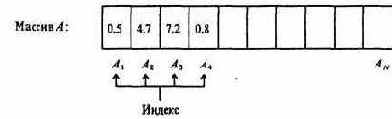
Рис. 1.32. Одномерный массив - набор элементов (компонентов)
Компонентами массива могут быть не только простейшие данные, но и структурные, в том числе массивы. В этом случае мы получаем массив массивов - многомерный массив. Для индексации элементарных компонент в этом случае может потребоваться два, три и более индексов.
В некоторых системах программирования существуют специальные виды массивов. Например, массив литер (символов) определяется как строка.
Данные, хранящиеся в массивах, находятся в оперативной памяти компьютера. Это, с одной стороны, ускоряет доступ к ним в ходе решения задачи, а с другой -налагает ограничения на объем возможной информации, организованной в виде массивов. Не следует поэтому, без крайней необходимости, создавать новые массивы для перемещения данных из уже существующих массивов.
Рассмотрим в качестве примера задачу сортировки набора некоторых данных, для которых имеют смысл отношения «больше» или «меньше». Представьте себе, что надо карточки в картотеке разместить в порядке возрастания записанных на них чисел. Используем для сортировки набора чисел (т.е. записи их в порядке возрастания) одномерный (линейный) массив. Дадим ему имя А,
тогда a1, a2, a3,..., аn - компоненты массива.
Существует огромное число методов сортировки массивов. Рассмотрим один из самых простых (но не самых быстрых) - метод выбора.
В начале процесса имеем заполненный числами массив (неотсортированный). Процесс сортировки строится по индукции. Допустим, мы уже отсортировали часть массива и имеем упорядоченную последовательность
a1 < a2
< … < ai-l
и оставшуюся неотсортированной последовательность
ai, ai+1,… aN.
При каждом шаге, начиная с i = 1, из неотсортированной части последовательности извлекается наименьший элемент х = ai, и меняется местами с i-м элементом.
Затем этот процесс повторяется для i = 2, i = 3 и т.д., до тех пор пока не останется один, самый большой элемент.
Этот алгоритм потребует многократного нахождения наименьшего элемента массива. Этот «вспомогательный» алгоритм поиска наименьшего среди аi, ... , аN может быть следующим:
1) фиксируется в качестве значения вспомогательной переменной т первый слева элемент массива: т = аi (в конце процесса т будет иметь значение наименьшего элемента);
2) выполняется сравнение т с элементом массива aj, (начиная с номера j = i + 1) и, если aj < т, то т заменяется на аj;
3) далее выполняется сравнение т с очередным элементом массива, т.е. j увеличивается на единицу и шаги 2, 3 выполняются снова, до тех пор пока у не достигнет максимального значения индекса элемента массива.
После выполнения этих предписаний переменная т будет соответствовать наименьшему элементу массива.
Двумерный массив визуально представляется плоской таблицей, табл. 1.10. При наличии одного имени (идентификатора) для всех компонентов каждый из них фиксируется значениями двух индексов, указывающих номер строки и номер столбца, на пересечении которых находится эта компонента.
Рассмотрим пример обработки данных, хранящихся в двумерном массиве. Допустим, что на некоторой территории (например, страны) «квадратно-гнездовым» способом расставлены температурные датчики, и их показания обраны в одном центре (что вполне близко к реальной деятельности метеослужбы). Тогда в таблицу - двумерный массив - попадут значения температуры tij
в сответствующих точках. Требуется, просматривая таблицу построчно, найти те точки (т.е. индексы узлов), между которыми температура принимает некоторое заданное значение Т.
Таблица 1.10 Графический образ двумерного массива
 |
1 |
2 |
3 |
4 |
… |
|
1 |
a11 |
a12 |
a13 |
a14 |
… |
|
2 |
a21 |
a22 |
a23 |
a24 |
… |
|
3 |
a31 |
a32 |
a33 |
a34 |
… |
|
4 |
a41 |
a42 |
a43 |
a44 |
… |
|
… |
… |
… |
… |
... |
… |
Пусть в таблице п
строк и т столбцов. Вспомогательным алгоритмом в данной задаче может быть алгоритм поиска нужных узлов в одной строке. Пусть эта строка имеет номер k. Алгоритмы записаны без комментариев для самостоятельного разбора.
Вспомогательный алгоритм (k):
1) положить j = 1;
2) если tk,j < T < tk.j+1, то см. п. 2;
3) увеличить j на 1,
4) если j < m, то вернуться к п. 2;
5) задача решена, ответ: (k,j), (k,j + 1);
6)конец.
Основной алгоритм:
1) положить k= 1;
2) выполнить вспомогательный алгоритм (K);
3) увеличить k
на 1;
4) если k > n,
то вернуться к п.2;
5)конец.
Записи, множества, файлы
Обобщением массива является комбинированный тип данных - запись, являющаяся неоднородной упорядоченной статической структурой прямого доступа. Запись есть набор именованных компонент - полей (часто разного типа), объединенных одним общим именем и идентифицируемых (адресуемых) с помощью как имени записи, так и имен полей, рис. 1.33.
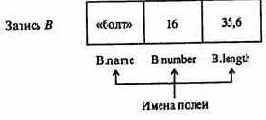
Рис. 1.33. Иллюстрация «записи».
Запись В
состоит из трех полей, имеющих последовательно типы «текст», «целое число», «вещественное число»: 1-е поле - название детали, 2-е - условный номер по каталогу, 3-е - длина. При работе с одной единственной записью (что бывает нечасто), имя поля можно использовать как обычную переменную, т.е. можно изменять значение поля с помощью операции присваивания или любых других операций, доступных над величинами данного типа. Если же данная запись - лишь часть набора данных, то имя поля состоит из двух частей и называется составным именем поля (на рис. 1.33 составные имена В. name, В. number, В. length).
Для облегчения работы с полями в различных языках программирования существуют средства, облегчающие их адресацию.
И записи, и массивы обладают одним общим свойством - произвольным доступом к компонентам. Записи более универсальны в том смысле, что для них не требуется идентичности типов их компонент. Массивы обеспечивают большую гибкость -индексы их компонент можно вычислять в отличие от имен полей записей.
Существенно иные возможности дает структура данных, моделирующая свойства математического объекта - множества.
Над множеством могут быть выполнены следующие операции:
1) объединение множеств (операция сложения '+');
2) пересечение множеств (операция умножения '*');
3) теоретико-множественная разность (вычитание множеств '-');
4) проверка принадлежности элемента множеству.
Различия между множеством и массивом очень существенны: размер множества заранее не оговаривается (хотя и ограничен компьютерной реализацией, например, 255), не существует иного способа доступа к элементам множества, кроме как проверкой принадлежности множеству.
Более сложной, чем рассмотренные выше из предусмотренных в современных системах программирования структур данных, является очередь (файл).
Понятие «файл» при всей своей привычности употребляется в информатике в нескольких не совсем совпадающих смыслах. Здесь мы остановимся лишь на представлении о файле как однородной упорядоченной динамической структуре последовательного доступа - очереди.
Очередь есть линейно упорядоченный набор следующих друг за другом компонент, доступ к которым происходит по следующим правилам:
1) новые компоненты могут добавляться лишь в хвост очереди;
2) значения компонент могут читаться (извлекаться) лишь в порядке следования компонент от головы к хвосту очереди.
Размер очереди заранее не оговаривается и теоретически может считаться бесконечным. Для запоминания (хранения) компонент очереди часто используют внешние запоминающие устройства большой емкости - магнитные диски и ленты. Отсюда другое название очереди - файл (по английски это слово имеет ряд значений, в том числе «картотека», «шеренга», «очередь»).
Исторически слово «файл» стало впервые применяться в информатике для обозначения последовательного набора каких-либо данных или команд (программа), хранящихся на внешнем запоминающем устройстве. Несколько позже были осознаны абстрактные, не зависящие от магнитных дисков и лент, свойства очереди как структуры данных, полезные при решении многих задач обработки - информации.
Такой принцип извлечения и добавления компонент к очереди часто; называется «первым вошел - первым вышел» (английская аббревиатура - «FIFO»), рис. 1.34.
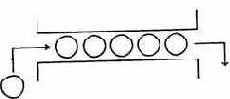
Рис. 1.34. Иллюстрация «очереди»
В языках программирования существуют и такие разновидности файлов, которые не подчиняются условию последовательности доступа к его компонентам (так называемые, файлы прямого доступа). Они уже не являются очередями.
Суперпозиция структур данных
Из рассмотренных структур данных можно создавать различные суперпозиции (вопрос о допустимости той или иной суперпозиции в конкретном языке программирования следует искать в его описании).
Рассмотрим в качестве примера такую часто используемую суперпозицию как файл записей - обычную, например, при создании баз данных. Итак, имеется файл по имени F, содержащий некоторое количество таких записей, как на рис. 1.30. Составим алгоритм подсчета количества болтов, у которых длина (length) заключена в пределах от 3 до 40:
1) положить k = 0 (в конце работы k - число искомых болтов);
2) прочесть первую запись из файла;
3) если В.name = 'болт' и 30 < B.lenght < 40, то увеличить k на 1;
4) если файл уже опустел, то идти к п. 7, иначе - к п. 5;
5) прочесть следующую запись из файла;
6) идти к п.З;
7) конец работы; k - число
искомых болтов.
Стек
Существует (и часто используется) и другая структура данных, в которой тот элемент, который первый в нее помещался, выходит последним и, наоборот, тот, который последним входит, выходит первым (английская аббревиатура «LIFO»). Такая структура получила название стек
(или магазин - по сходству с магазином стрелкового оружия), рис. 1.35.
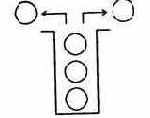
Рис. 1 35. Иллюстрация «стека»
Стеки и принцип LIFO находят очень широкое применение в информатике. Рассмотрим в качестве примера использование стека при вычислении значения арифметического выражения.
Вычисление значения выражения требует соблюдения старшинства операций. Операции по старшинству при вычислении значений математических выражений располагаются в следующем порядке: вычисление значений функций (включая возведения в степень), умножения и деления, сложения и вычитания.
Изменить такой «естественный» порядок операций можно с помощью скобок.
Например, вычисление известного из школьного курса математики выражения b2-
4*а*с включает предварительное установление порядка выполнения операций:
14 2 3
b2 – 4*a*c
Для этого выражение просматривают несколько раз. Выполнение каждой операции дает некоторое число, которое приходится записывать отдельно от выражения, запоминая тот фрагмент выражения, для которого число является значением.
Сейчас рассмотрим экономный алгоритм вычисления значения выражения, использующий два магазина для перестановки элементов выражения (с учетом старшинства операций) и для хранения промежуточных результатов. Магазины обозначим M1 и М2, в M1
будут попадать знаки операций, в М2
- числа, участвующие в записи выражения, значения переменных и все промежуточные числовые значения.
Ограничимся выражениями, состоящими только из чисел и переменных без индекса, связанных знаками операций, *, /, +, -. Знак «минус» будет знаком лишь двухместной операции вычитания, выражения типа « - а + I» исключаются из рассмотрения. От этих ограничений можно было бы и отказаться, но это удлинило бы изложение. Пока предположим также, что в выражении нет скобок.
Опишем алгоритм вычисления. Исходное выражение читается слева направо; если прочитано число, то оно заносится в M2, если переменная - в М2 заносится ее значение; если же прочитан знак операции, то необходимо различать несколько случаев.
1) М1 пуст; прочитанный знак помещается на вершину М1.
2) прочитанный знак помещается на вершину M1, если он обозначает операцию, которая старше и поэтому должна выполняться до операции, знак которой был расположен на вершине М1.
3) если операции равноправны или если та, знак которой только что прочитан в выражении, должна выполняться позднее, необходимо применить операцию, знак которой расположен на вершине M1, к двум верхним числам из М2 (число на вершине - второй операнд, число под ним - первый); знак операции на вершине M1 удаляется из M1,
вместо двух верхних чисел в M2
помещается результат выполнения над ними операции.
В некоторый момент в исходном выражении не остается символов. Если пуст и M1,
то вычисление окончено, результат находится в M2; в противном случае знаки операции извлекаются по очереди из M1
и соответствующие операции применяются к числам из M2.
Рассмотрим вычисление выражения b2 - 4*а*с; значения переменных а, b, с обозначим А, В, С. Знак возведения в степень обозначим, как часто делается, стрелкой вверх.


Про знак операции говорят, что он имеет более высокий приоритет в сравнении с другим знаком, если обозначаемая им операция старше. В других случаях говорят о равных приоритетах или более низком приоритете. Рассмотренные знаки операций распадаются на группы равных по приоритету:
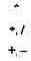
Группы упорядочены по убыванию приоритета.
Теперь дадим правило работы со скобками. Левая скобка заносится в M1
сразу после прочтения. Прочтение правой скобки влечет выполнение всех операций, знаки которых находятся в Mi
выше левой скобки; после выполнения этих операций обе скобки уничтожаются. Вот что будет происходить при выполнении (а + b) * с:

Иерархическая организация данных
Во всех рассмотренных выше структурах отдельные элементы (компоненты, поля, составляющие) структуры были формально равноправны. Существует, однако, широкий круг задач, в которых одни данные естественным образом «подвязаны» к другим. В этом случае возникает соподчиненная (иерархическая) структура данных. Ограничимся конкретным примером. Представим себе генеалогическое дерево, корень которого - имя человека, на следующем уровне - имена его родителей, еще на следующем - имена родителей родителей и т.д. Такая структура называется двоичным деревом, рис. 1.36.
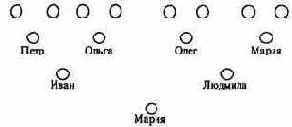
Рис. 1.36. Структура типа «двоичное дерево»;
пара ближайших по горизонтали кружков -мужское и женское имя
Как структурировать эти данные (имена)? Для помещения их в текстовый массив и запись трудно придумать логически оправданный порядок следования.Самое разумное - создать динамическую структуру типа той, что изображена на рис. 1.36. современные языки программирования позволяют это делать и обрабатывать такие структуры с высокой эффективностью.