РЕКУРСИВНЫЕ ФУНКЦИИ
Еще одним подходом к проблеме формализации понятия алгоритма являются, так называемые, рекурсивные функции. Исторически этот подход возник первым, поэтому в математических исследованиях, посвященных алгоритмам, он имеет наибольшее распространение.
Рекурсией называется способ задания функции, при котором значение функции при определенном значении аргументов выражается через уже заданные значения функции при других значениях аргументов. Применение рекурсивных функций в теории алгоритмов основано на идее нумерации слов в произвольном алфавите последовательными натуральными числами. Таким образом любой алгоритм можно свести к вычислению значений некоторой целочисленной функции при целочисленных значениях аргументов.
Введем несколько основных понятий. Пусть X, Y - два множества. Частичной функцией (или отображением) из Х в Y будем называть пару <D(f), f>, состоящую из подмножества D(f) Ì X
(называемого областью определения f)
и отображения f: D(f)
® Y. Если D(f)
пусто, то f нигде не определена. Будем считать, что существует единственная нигде не определенная частичная функция.
Через N
будем обозначать множество натуральных чисел. Через (N)n
(при п ³ 1) будем обозначать n-кратное декартово произведение N на себя, т.е. множество упорядоченных n-ок (х1 ..., xn), хi Ì N. Основным объектом дальнейших построений будут частичные функции из (N)m в (N)n для различных т и п.
Частичная функция f из (N)m
в (N)n называется вычислимой, если можно указать такой алгоритм («программу»), который для входного набора х Ì (N)m дает на выходе f(x), если х Ì D(f) и нуль, если х Ë
D(f). В этом определении неформальное понятие алгоритма (программы) оказывается связанным (отождествленным) с понятием вычислимости функции. Вместо алгоритмов далее будут изучаться свойства вычислимых функций. Вместо вычислимых функций оказывается необходимым использовать более широкий класс функций (и более слабое определение) - полувычислимые функции.
Частичная функция из (N)" в (N)" полувычислима, если можно указать такой алгоритм (программу), который для входного набора х с (N)" дает на выходе х е D(f),
или алгоритм работает неопределенно долго, если х е D(f). Очевидно, что вычислимые функции полувычислимы, а всюду определенные полувычислимые функции вычислимы.
Частичная функция f называется невычислимой, если она не является ни вычислимой, ни полувычислимой.
Из вновь введенных понятий основным является полувычислимость, так как вычислимость сводится к нему. Существуют как невычислимые функции, так и функции, являющиеся полувычислимыми, но не вычислимые. Пример такой функции:

Можно показать, что существует такой многочлен с целыми коэффициентами P(t, x1,...,xn), что g(t) - невычислима. Однако, легко видеть, что g(t) - полувычислима.
Фундаментальным открытием теории вычислимости явился, так называемый, тезис Черча, который в слабейшей форме имеет следующий вид: можно явно указать а) семейство простейших полувычислимых функций; б) семейство элементарных операций, которые позволяют строить по одним полувычислимым функциям другие полувычислимые функции с тем свойством, что любая полувычислимая функция получается за конечное число шагов, каждый из которых состоит в применении одной из элементарных операций к ранее построенным или к простейшим функциям.
Простейшие функции:
suc: N ® N; suc(x) = x+1 - определение следующего за х
числа;
l(n): (N)n ®
N; l(n) (x1,..., хn) = 1, п ³ 0 - определение «размерности» области определения функции;
рr

N; pr

1 - «проекция» области определения на одну из переменных.
Элементарные операции над частичными функциями:
а) композиция
(или подстановка) ставит в соответствие паре функций f из (N)m в (N)n и g из (N)n
в (N)p функцию h = gof из (N)m в (N)p , которая определяется как
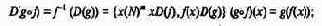
б) соединение
ставит в соответствие частичным функциям fi из (N)ni, i = 1, ..., k функцию (fi, ..., fk) из (N)m в (N)n1
х... х (N)nk, которая определяется как
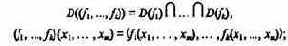
в) рекурсия
ставит в соответствие паре функций f из (N)n в N и g
из (N)n+2 в N функцию h
из (N)n+2 в N, которая определяется рекурсией по последнему аргументу
h(x1,... , хn, 1) = f (x1,... ,xп) (начальное условие),
h (x1,... ,хn, k+1) = g(x1,... ,xn, k, h(x1,... ,хn, k)) при k ³ 1 (рекурсивный шаг).
Область определения D(h) описывается также рекурсивно:
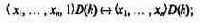
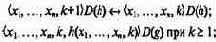
г) операция т,
которая ставит в соответствие частичной функции f из (N)n+1 в N частичную функцию h из (N)n в N, которая определяется как

Операция т
позволяет вводить в вычисления перебор объектов для отыскания нужного в бесконечном семействе.
Теперь, когда введены простейшие функции и элементарные операции, можно дать следующие основные определения:
а) последовательность частичных функций fi, . . . ,fN называют частично рекурсивным (соответственно примитивно рекурсивным) описанием функции fN = f, если fi - одна из простейших функций; fi
для всех i ³ 2 либо является простейшей функцией, либо получается применением одной из элементарных операций к некоторым из функций fi,..., fi-1 (соответственно одной из элементарных операций, кроме т);
б) функция f называется частично рекурсивной (соответственно примитивно рекурсивной), если она допускает частично рекурсивное (соответственно примитивно рекурсивное) описание.
Теперь можно привести тезис Черча в обычной форме:
а) функция f полувычислима, если и только если она частично рекурсивна;
б) функция f вычислима, если и только если рекурсивны f и характеристическая функция XD(f).
Характеристическая функция подмножества Х в Y(X Ì Y) есть такая функция, что
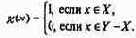
Тезис Черча может использоваться как определение алгоритмической неразрешимости.
Пусть имеется счетная последовательность «задач» P1, P2, ..., которые имеют ответ «да» или «нет». Такая последовательность носит название «массовой проблемы». Свяжем с ней функцию f из N в N:
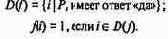
Массовая проблема Р
называется алгоритмически разрешимой, если функции f и XD(f) частично рекурсивны. В противном случае Р называется алгоритмически неразрешимой.