ОСНОВНЫЕ ПОНЯТИЯ
Такая структура, как
граф (в качестве синонима используется также термин «сеть») , имеет самые различные применения в информатике и в смежных прикладных областях, поэтому познакомимся с основными понятиями теории графов.
Граф G = (V, Е) задается парой конечных множеств V и Е. Элементы первого множества V1, v2,..., vM называются вершинами графа (при графическом представлении им соответствуют точки). Элементы второго множества е1, е2, ...,eN
называют ребрами. Каждое ребро определяется парой вершин (при графическом представлении ребро соединяет две вершины графа). Если ребра графа определяются упорядоченными парами вершин, то такой граф называют ориентированным
(на чертеже при изображении ориентированного графа на каждом ребре ставят стрелку, указывающую его направление). Ориентированный граф с пятью вершинами и семью ребрами изображен на рис. 1.6.
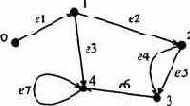
Рис. 1.6. Пример ориентированного графа
Если две вершины соединены двумя или более ребрами, то эти ребра называют параллельными (например, ребра е4 и е5). Если начало и конец ребра совпадают, то такое ребро называется петлей
(например, ребро е7). Граф без петель и параллельных ребер называется простым.
Если ребро ek определяется вершинами vi и vj (будем обозначать этот факт следующим образом: ek = (vi, vj), то говорят, что ребро ek инцидентно
вершинам vi и vj. Две вершины vi и vj называются смежными, если в графе существует ребро (vi, vj).
Последовательность вершин vi1, vi2,..., vik, таких, что каждая пара (vi,(j-1), vij) при 1 < j ? k
определяет ребро, называется маршрутом
в графе G. Вершины vil и vik называют концевыми
вершинами маршрута, все остальные входящие в него вершины - внутренними.
Маршрут, в котором все определяемые им ребра различны, называют цепью. Цепь считают замкнутой, если ее концевые вершины совпадают. Замкнутая цепь, в которой все вершины (за исключением концевых) различны, называется циклом. Незамкнутая цепь, в которой все вершины различны, носит название путь.
Если в ориентированном графе существует путь из vi в vj,
то говорят, что вершина vj достижима из вершины vi.
Две вершины vi
и vj называют связанными в графе G, если в нем существует путь, для которого эти вершины являются концевыми. Граф G
называется связным, если каждые две вершины в нем являются связанными. На рис. 1.7 изображен простой неориентированный связный граф.
Последовательность вершин v1, v5, i4, v3 , например, определяет путь, а последовательность вершин v1, v5,
i4, v3, vl, v1 - цикл. Деревом будем называть неориентированный связный граф без циклов. Лес - это любой граф без циклов. На рис. 1.8 показаны возможные деревья с пятью вершинами.
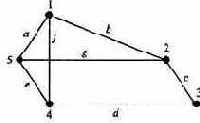
Рис. 1.7. Пример неориентированного связного графа
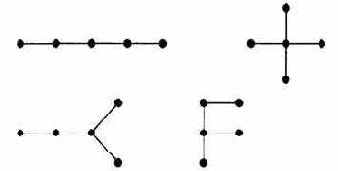
Рис. 1.8. Примеры деревьев
Анализ приведенных здесь понятий и определений показывает, что в качестве моделей графы удобно использовать в тех случаях, когда рассматривается система каких-либо объектов, между которыми существуют определенные связи, отношения, когда изучается структура системы, возможности ее функционирования. В информатике графы используются в разделах: операционные системы, алгоритмизация, структуры данных, информационное моделирование и др.