ДИНАМИКА ЧИСЛЕННОСТИ ПОПУЛЯЦИЙ ХИЩНИКА И ЖЕРТВЫ
Рассматривая динамику численности популяций хищника и жертвы, экологи прежде всего стремятся понять ее закономерности и разъяснить различия между типами динамик. В простейших моделях хищник и жертва рассматриваются безотносительно влияния на них других видов. Одна из самых первых и простых моделей была предложена, как и модель межвидовой конкуренции, Лоткой и Вольтеррой, и носит их имя.
Модель состоит из двух компонентов: С
- численность популяции хищника и N -численность популяции жертвы.
Предполагается, что в отсутствие хищника популяция жертвы растет экспоненциально. Чем больше численность той и другой популяции, тем чаще происходят встречи. Число встреченных и съеденных жертв будет зависеть от эффективности, с которой хищник находит и ловит жертву. Если обозначить через а'
«эффективность поиска», то скорость поедания жертвы будет равна a'•C•N, и окончательно для численности жертвы
получаем
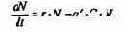
В отсутствие пищи отдельные особи хищника голодают и гибнут. Предположим вновь, что численность хищника в отсутствие пищи будет уменьшаться экспоненциально:
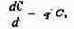
(q - смертность). Скорость рождения новых особей в данной модели полагается зависящей от двух обстоятельств: скорости потребления пищи
a'•C•N, и эффективности f, с которой эта пища переходит в потомство хищника. Итак, для численности хищника окончательно получаем
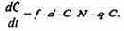
Так как процессы надо рассматривать вместе, объединим уравнения в систему:
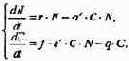
Как и в предыдущем пункте, свойства этой модели можно исследовать, построив изоклины.
Для жертвы имеем
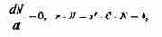
или, выражая С, получаем
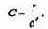
Соответствующее уравнение изоклины для популяции хищника
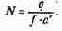
Если поместить обе изоклины на одном рисунке, получим картину взаимодействия популяций (рис. 7.46).
Как видно на рис. 7.47, численности популяций хищника и жертвы совершают периодические колебания: при увеличении численности хищников уменьшается
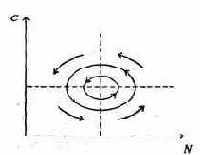
Рис. 7.46. Динамика численности популяции хищника и жертвы. Численность обеих популяций совершает периодические колебания
численность популяции жертвы и наоборот. Такие колебания численности будут продолжаться в соответствии с моделью до тех пор, пока какое-либо внешнее воздействие не изменит численность популяций, после чего произойдет переход в новое устойчивое состояние (такая ситуация называется «нейтральные устойчивые циклы»).
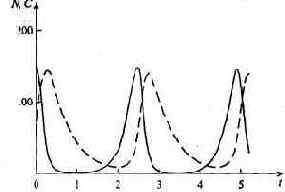
Рис. 7.47. Динамика численности популяции хищника и жертвы при r = 5, а' = 0,1, q = 2, f = 0,6, N0 = 150, C0 = 50. Сплошная линия - численность жертвы, штриховая – хищника